LeetCode-97-交错字符串
Miyagi Lv1
 2021-02-04 15:14:27      642 字  3 分钟  

题目地址（LeetCode-97）

https://leetcode-cn.com/problems/interleaving-string/

题目描述

1
2
3
4
5
6
7
8
9
给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
提示：a + b 意味着字符串 a 和 b 连接。

示例1:

1
2
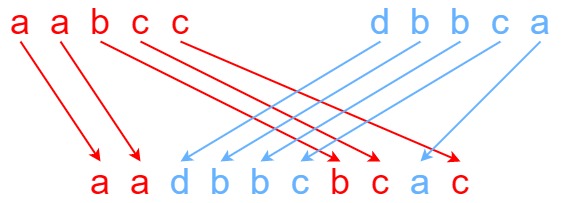
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例2:

1
2
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例3:

1
2
输入：s1 = "", s2 = "", s3 = ""
输出：true

解法

采用动态规划的思想，dp[i][j]表示s1从0到i-1的子字符串和s2从0到j-1的子字符串能否组成s3从0到i+j-1的字符串。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int len1 = s1.length(), len2 = s2.length(), len3 = s3.length();
        if (len1 + len2 != len3) {
            return false;
        }
        // 表示 s1[0...i-1] 和 s2[0...j-1] 能否组成交叉字符串 s3[0...i+j-1]
        boolean[][] dp = new boolean[len1 + 1][len2 + 1];
        dp[0][0] = true;
        // 考虑s2为空的情况
        for (int i = 1; i <= len1; i++) {
            dp[i][0] = s1.charAt(i - 1) == s3.charAt(i - 1) && dp[i - 1][0];
        }
        // 考虑s1为空的情况
        for (int i = 1; i <= len2; i++) {
            dp[0][i] = s2.charAt(i - 1) == s3.charAt(i - 1) && dp[0][i - 1];
        }

        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                dp[i][j] = dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)
                        || dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1);
            }
        }
        return dp[len1][len2];
    }
}

Runtime beats: 66.87%
Memory usage beats: 98.20%

讨论区解法

该解法利用DFS，用invalid[i][j]数组记录s1[0~i]和s2[0~j]能否组成交错数组。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        char[] c1 = s1.toCharArray(), c2 = s2.toCharArray(), c3 = s3.toCharArray();
        int m = s1.length(), n = s2.length();
        if(m + n != s3.length()) return false;
        return dfs(c1, c2, c3, 0, 0, 0, new boolean[m + 1][n + 1]);
    }
    
    public boolean dfs(char[] c1, char[] c2, char[] c3, int i, int j, int k, boolean[][] invalid) {
        if(invalid[i][j]) return false;
        if(k == c3.length) return true;
        boolean valid = 
            i < c1.length && c1[i] == c3[k] && dfs(c1, c2, c3, i + 1, j, k + 1, invalid) || 
            j < c2.length && c2[j] == c3[k] && dfs(c1, c2, c3, i, j + 1, k + 1, invalid);
        if(!valid) invalid[i][j] = true;
        return valid;
    }
}

Runtime beats: 89.92%
Memory usage beats: 22.57%

 评论